RBM Visualizations

Renders from March 06, 2014.

Something interesting that Hinton has proposed is that we can take a look about what machines "dream about" in their sleep state.

In the spirit of reproducing good research to baseline our implementation, we've visualized our RBMs based on the techniques from Yosinski and Lipson's paper:

Below is a sampling from the renders taken from our Deep Learning implementation of Restricted Boltzmann Machines in Metronome. In these renders the RBMs are learning reprensetations of the canonical MNIST Dataset. As you can see in the learned filter, portions of digits are clearly visible.

Filter Renders

...we plot the learned filter for each hidden neuron, one per column of W. Each filter is of the same dimension as the input data, and it is most useful to visualize the filters in the same way as the input data is visualized. In the cases of image patches, we show each filter as an image patch...

Starting state for filters	Filters at 206 Cross Entropy	Filters at 4.9 Cross Entropy

Activation Renders

...we plot this probability of activation for each hidden neuron...

At Initialization Time:

At 206 Cross Entropy:

At 78 Cross Entropy:

At 4.9 Cross Entropy:

Weight Histogram Renders

A look at how the connection weights in the RBMs change during training in the form of a weight histogram.

At Initialization Time:

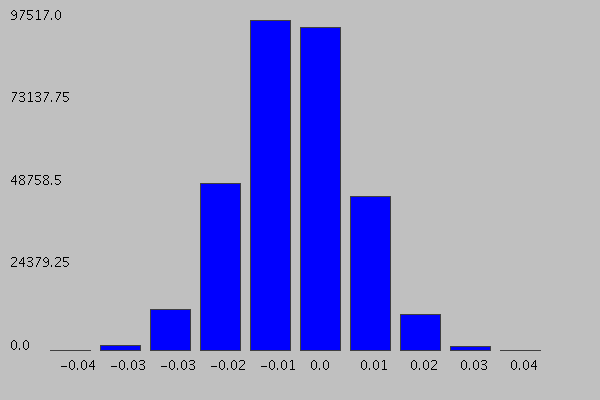
At 4.9 Cross Entropy:

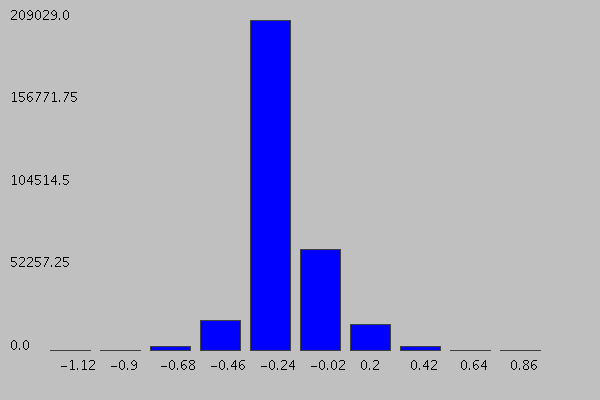
The Dream State of a Machine

So what do all these visualization drive? What we want from the RBMs in Deep Learning is for them to learn progressively higher level representations of the input dataset in the pre-train phase. So we want to know what the machine "dreams" when we stimulate it with a certain input.

Take a look at how Hinton explains the dream states of RBMs:

Cross Entropy	The "0" Digit	The "1" Digit	The "3" Digit	The "5" Digit	The "9" Digit
Input Data
Cross Entropy 206
Cross Entropy 140
Cross Entropy 78
Cross Entropy 4

If this kind of ML is your cup of tea then take a minute to Vote for us at Hadoop Summit 2014!